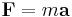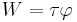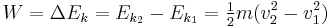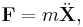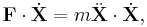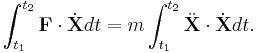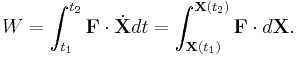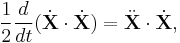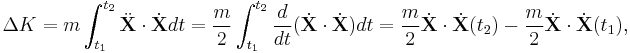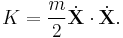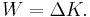Work (physics)

Classical mechanics
$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics
Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics
Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Euler's laws of motion · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement
Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson

Work
SI symbol:	W
SI unit:	joule
Derivations from other quantities:	W = F · d W = τ θ

In physics, (mechanical) work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work. The term work was first coined in 1826 by the French mathematician Gaspard-Gustave Coriolis.^[1]^[2]

If a constant force of magnitude F acts on a point that moves s in the direction of the force, then the work W done by this force is calculated W=Fs. For example, if a force of 10 newtons (F=10 N) acts along a path of 2 metres (s =2 m), it will do work W equal to W =(10 N)(2 m) = 20 N*m =20 J, where joule (J) is the SI unit for work (defined as the product N*m, so that a joule is a newton-meter).

For moving objects, the quantity of work/time enters calculations as distance/time, or velocity. Thus, at any instant, the rate of the work done by a force (measured in joules/second, or watts) is the scalar product of the force (a vector) with the velocity vector of the point of application. This scalar product of force and velocity is called instantaneous power. Just as velocities may be integrated over time to obtain a total distance, by the fundamental theorem of calculus, the total work along a path is similarly the time-integral of instantaneous power applied along the trajectory of the point of application.

The first law of thermodynamics states that when work is done to a system (and no other energy is subtracted in other ways), the system's energy state changes by the same amount of the work input. This equates work and energy. In the case of rigid bodies, Newton's laws can be used to derive a similar relationship called the work-energy theorem.

1 Units
2 Mathematical calculation
- 2.1 Force and displacement
- 2.2 Torque and rotation
3 Work and kinetic energy
4 Frame of reference
5 Zero work
6 References
7 Bibliography
8 External links

Units

Mathematical calculation

Calculating the work as "force times straight path segment" can only be done in the simple circumstances described above. If the force is changing, if the body is moving along a curved path, possibly rotating and not necessarily rigid, then only the path of the application point of the force is relevant for the work done, and only the component of the force parallel to the application point velocity is doing work (positive work when in the same direction, and negative when in the opposite direction of the velocity). This component of the force can be described by the scalar quantity called scalar tangential component (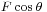 $\scriptstyle F\cos\theta$ , where 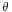$\scriptstyle \theta$ is the angle between the force and the velocity). And then the most general definition of work can be formulated as follows:

Work of a force is the line integral of its scalar tangential component along the path of its application point.

Simpler (intermediate) formulas for work and the transition to the general definition are described in the text below.

Force and displacement

If a force F that is constant with respect to time acts on an object while the object is translationally displaced for a displacement vector d, the work done by the force on the object is the dot product of the vectors F and d:^[3]

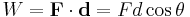$W = \bold{F} \cdot \bold{d} = F d \cos\theta$ (1)

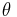where $\textstyle\theta$ is the angle between the force and the displacement vector.

Whereas the magnitude and direction of the force must remain constant, the object's path may have any shape: the work done is independent of the path and is determined only by the total displacement vector 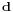$\scriptstyle\bold{d}$ . A most common example is the work done by gravity – see diagram. 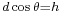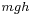The object descends along a curved path, but the work is calculated from $\scriptstyle d \cos\theta = h$ , which gives the familiar result $\scriptstyle mgh$ .

More generally, if the force causes (or affects) rotation of the body, or if the body is not rigid, displacement of the point to which the force is applied (the application point) must be used to calculate the work. This is also true for the case of variable force (below) where, however, magnitude of 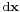$\scriptstyle \mathrm{d}\bold{x}$ can equally be interpreted as differential displacement magnitude or differential length of the path of the application point. (Although use of displacement vector most frequently can simplify calculation of work, in some cases simplification is achieved by use of the path length, as in the work of torque calculation below.)

In situations where the force changes over time, equation (1) is not generally applicable. But it is possible to divide the motion into small steps, such that the force is well approximated as being constant for each step, and then to express the overall work as the sum over these steps. This will give an approximate result, which can be improved by further subdivisions into smaller steps (numerical integration). The exact result is obtained as the mathematical limit of this process, leading to the general definition below.

The general definition of mechanical work is given by the following line integral:

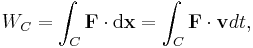$W_C = \int_{C} \bold{F} \cdot \mathrm{d}\bold{x} = \int_{C}\bold{F}\cdot \bold{v}dt,$ (2)

where:

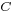$\textstyle _C$ is the path or curve traversed by the application point of the force;

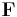$\bold F$ is the force vector;

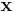$\bold x$ is the position vector; and

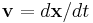$\bold{v} = d\bold{x}/dt$ is its velocity.

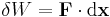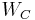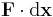The expression $\delta W = \bold{F} \cdot \mathrm{d}\bold{x}$ is an inexact differential which means that the calculation of $\textstyle{ W_C}$ is path-dependent and cannot be differentiated to give $\bold{F} \cdot \mathrm{d}\bold{x}$ .

Equation (2) explains how a non-zero force can do zero work. The simplest case is where the force is always perpendicular to the direction of motion, making the integrand always zero. This is what happens during circular motion. However, even if the integrand sometimes takes nonzero values, it can still integrate to zero if it is sometimes negative and sometimes positive.

The possibility of a nonzero force doing zero work illustrates the difference between work and a related quantity, impulse, which is the integral of force over time. Impulse measures change in a body's momentum, a vector quantity sensitive to direction, whereas work considers only the magnitude of the velocity. For instance, as an object in uniform circular motion traverses half of a revolution, its centripetal force does no work, but it transfers a nonzero impulse.

Torque and rotation

Work done by a torque can be calculated in a similar manner, as is easily seen when a force of constant magnitude is applied perpendicularly to a lever arm. After extraction of this constant value, the integral in equation (2) gives the path length of the application point, i.e. the circular arc $\ s$ , and the work done is 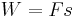$\ W=Fs$ .

However, the arc length can be calculated from the angle of rotation 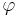$\varphi\;$ (expressed in radians) as 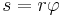$\ s= r \varphi\;$ , and the ensuing product 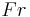$\ Fr \;$ is equal to the torque 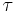$\tau\;$ applied to the lever arm. Therefore, a constant torque does work as follows:

$W= \tau \varphi\$

Work and kinetic energy

According to the work-energy theorem, if one or more external forces act upon a rigid object, causing its kinetic energy to change from E_k1 to E_k2, then the work (W) done by the net force is equal to the change in kinetic energy. For translational motion, the theorem can be specified as:^[4]

$W = \Delta E_k = E_{k_2} - E_{k_1} = \tfrac12 m (v_2^2 - v_1^2) \,\!$

where m is the mass of the object and v is the object's velocity.

The theorem is particularly simple to prove for a constant force acting in the direction of motion along a straight line. For more complex cases, however, it can be for variable force, we can use integration to get the same result. In rigid body dynamics, a formula equating work and the change in kinetic energy of the system is obtained as a first integral of Newton's second law of motion.

To see this, consider a particle P that follows the trajectory X(t) with a force F acting on it. Newton's second law provides a relationship between the force and the acceleration of the particle as

$\mathbf{F}=m\ddot{\mathbf{X}},$

where m is the mass of the particle.

The scalar product of each side of Newton's law with the velocity vector yields

$\mathbf{F}\cdot\dot{\mathbf{X}} = m\ddot{\mathbf{X}}\cdot\dot{\mathbf{X}},$

which is integrated from the point X(t₁) to the point X(t₂) to obtain

$\int_{t_1}^{t_2} \mathbf{F}\cdot\dot{\mathbf{X}} dt = m\int_{t_1}^{t_2}\ddot{\mathbf{X}}\cdot\dot{\mathbf{X}}dt.$

The left side of this equation is the work of the force as it acts on the particle along the trajectory from time t₁ to time t₂. This can also be written as

$W = \int_{t_1}^{t_2} \mathbf{F}\cdot\dot{\mathbf{X}} dt = \int_{\mathbf{X}(t_1)}^{\mathbf{X}(t_2)} \mathbf{F}\cdot d\mathbf{X}.$

This integral is computed along the trajectory X(t) of the particle and is therefore path dependent.

The right side of the first integral of Newton's equations can be simplified using the identity

$\frac{1}{2}\frac{d}{dt}(\dot{\mathbf{X}}\cdot \dot{\mathbf{X}}) = \ddot{\mathbf{X}}\cdot\dot{\mathbf{X}},$

which can be integrated explicitly to obtain the change in kinetic energy,

$\Delta K = m\int_{t_1}^{t_2}\ddot{\mathbf{X}}\cdot\dot{\mathbf{X}}dt = \frac{m}{2}\int_{t_1}^{t_2}\frac{d}{dt}(\dot{\mathbf{X}}\cdot \dot{\mathbf{X}}) dt = \frac{m}{2}\dot{\mathbf{X}}\cdot \dot{\mathbf{X}}(t_2) - \frac{m}{2}\dot{\mathbf{X}}\cdot \dot{\mathbf{X}} (t_1),$

where the kinetic energy of the particle is defined by the scalar quantity,

$K = \frac{m}{2}\dot{\mathbf{X}}\cdot \dot{\mathbf{X}}.$

The result is the work-energy principle for rigid body dynamics,

$W = \Delta K. \!$

This derivation can be generalized to arbitrary rigid body systems.

Frame of reference

The work done by a force acting on an object depends on the choice of reference frame because displacements and velocities are dependent on the reference frame in which the observations are being made.^[5]

The change in kinetic energy also depends on the choice of reference frame because kinetic energy is a function of velocity. However, regardless of the choice of reference frame, the work energy theorem remains valid and the work done on the object is equal to the change in kinetic energy.^[6]

Zero work

An important class of forces in mechanical systems perform zero work. These are constraint forces that restrict the relative movement of bodies. For example, the centripetal force exerted by a string on a ball in uniform circular motion does zero work because this force is perpendicular to the velocity of the ball. As a result the kinetic energy of the moving ball doesn't change.

Another example is a book at rest on a table, the table does no work on the book despite exerting a force equivalent to mg upwards, because no energy is transferred into or out of the book. On the other hand, if the table moves upward, then it performs work on the book, since the force of the table on the book will be acting through a distance.

A current that generates a magnetic field can also produce a magnetic force where a charged particle exerts a force on a magnetic field, but the magnetic force can do no work because the charge velocity is perpendicular to the magnetic field and in order for a force or an object to perform work, the force has to be in the same direction as the distance that it moves.

References

^ Jammer, Max (1957). Concepts of Force. Dover Publications, Inc.. ISBN 0-486-40689-X.
^ Sur une nouvelle dénomination et sur une nouvelle unité à introduire dans la dynamique, Académie des sciences, August 1826
^ Resnick, Robert and Halliday, David (1966), Physics, Section 7-2 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
^ Tipler (1991), page 138.
^ Resnick, Robert and Halliday, David (1966), Physics, Section 1-3 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
^ Resnick, Robert and Halliday, David, Physics, Section 4-6

Bibliography

Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed. ed.). Brooks/Cole. ISBN 0-534-40842-7.
Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd ed., extended version ed.). W. H. Freeman. ISBN 0-87901-432-6.

External links

Work – a chapter from an online textbook